http://en.wikipedia.org/wiki/Newton's_method

사이트 로그인
http://en.wikipedia.org/wiki/Newton's_method

계산기는 거들 뿐
혹은
계산기를 거들 뿐



http://kin.naver.com/qna/detail.nhn?d1id=11&dirId=1113&docId=221245100
다음 연립방정식의 해를 구하라(단, 해들은 모두 소수점 이하 9째 자리까지 표기)
y=x^2 과 y=e^(-x). 초기값=2

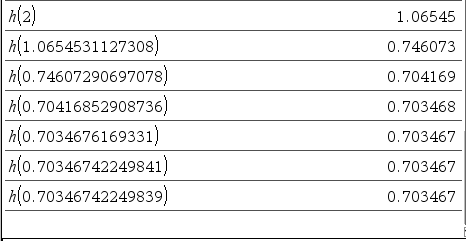
처음에만 h(2) 이후에는 h(ans) ctrl + enter

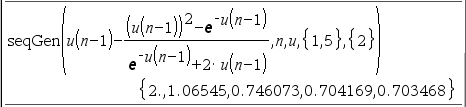
ctrl+ENTER 로 구할 것

9860G Recur 모드 이용
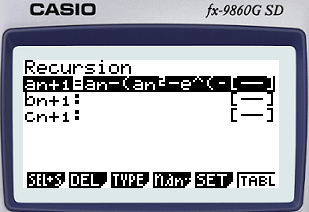
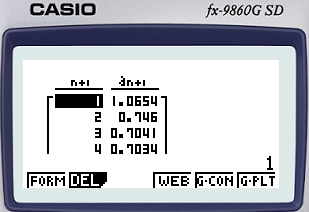
Square root of a number[edit]
Consider the problem of finding the square root of a number. Newton's method is one of many methods of computing square roots.
For example, if one wishes to find the square root of 612, this is equivalent to finding the solution to
The function to use in Newton's method is then,
with derivative,
With an initial guess of 10, the sequence given by Newton's method is
where the correct digits are underlined. With only a few iterations one can obtain a solution accurate to many decimal places.