- 세상의 모든 계산기 수학, 과학, 공학 이야기 기타 ()
Elo Rating System 이란?
1. 정의
승/패로 나뉘는 시합에 있어서, 선수의 실력을 (승/패, 승률에 따라) 점수화하여 순위를 매기는 방식.
https://en.wikipedia.org/wiki/Elo_rating_system
https://namu.wiki/w/Elo%20%EB%A0%88%EC%9D%B4%ED%8C%85
2. 특징
- 이기면 레이팅이 오른다.
레이팅이 자기보다 높은 사람에게 이기면 확 오른다.
레이팅이 자기보다 낮은 사람에게 이기면 조금 오른다. - 지면 레이팅이 떨어진다.
레이팅이 자기보다 높은 사람에게 지면 조금 떨어진다.
레이팅이 자기보다 낮은 사람에게 지면 많이 떨어진다. - 이기고 레이팅이 떨어진다거나, 지고 레이팅이 올라간다거나 하는 일은 절대 없음!
- 레이팅을 기반으로 플레이어간 상대 승률을 추정할 수 있다.

경기 결과에 따른 레이팅 변화
ㄴ Ra : 기존 레이팅
ㄴ K : factor
ㄴ Sa : 실제 획득 점수 (승=1, 무승부=0.5, 패=0)
ㄴ Ea : 기대 획득 점수 (=Elo 기반 승률)

<검은 색 곡선은 y축_좌 승률, 브라운(K=32)과 레드(K=16) 곡선은 y축_우 점수변공>
Graphs of probabilities and Elo rating changes (for K=16 and 32) of expected outcome (solid curve) and unexpected outcome (dotted curve) vs initial rating difference For example, player A starts with a 1400 rating and B with 1800 in a tournament using K = 32 (brown curves). The blue dash-dot line denotes the initial rating difference of 400 (1800 - 1400). The probability of B winning, the expected outcome, is 0.91 (intersection of black solid curve and blue line); if this happens, A's rating decreases by 3 (intersection of brown solid curve and blue line) to 1397 and B's increases by the same amount to 1803. Conversely, the probability of A winning, the unexpected outcome, is 0.09 (intersection of black dotted curve and blue line); if this happens, A's rating increases by 29 (intersection of brown dotted curve and blue line) to 1429 and B's decreases by the same amount to 1771.
- 플레이어 A = 1400, 플레이어 B = 1800, 점수(rating)차이 400.
- K=32 인 것으로 계산시
B가 이기면 Expected 해당 (확률 0.91 = 91%)
A 점수 3점 깍임 = 1400 - 3 = 1397
B 점수 3점 오름 = 1800 + 3 = 1803
A가 이기면 Unexpected 해당 (확률 0.09 = 9%)
A 점수 = 1400 + 29 = 1429
B 점수 = 1800 - 29 = 1771
3. 장/단점
댓글3
-
세상의모든계산기
A, B, C 선수만 존재하는 풀을 가정해 보겠습니다.
C는 A와도 경기를 해 보았고, B와도 경기를 해 보았습니다만, A와 B는 지금까지 직접 경기를 해 본 적이 없습니다.- A의 C에 대한 1:1 승률은 99.959278561331%로 ELO Rating 1356점의 차이가 납니다.
- B의 C에 대한 1:1 승률은 91.190530760341%로 ELO Rating 406점의 차이가 납니다.
- A는 B보다 Elo Rating 으로 +950 높으므로 승률이 99.580074308528% 가 될 것으로 추정해 볼 수 있지만,
막상 A vs B 를 1:1로 붙여보면 A의 승률이 80%에 불과합니다.
(B가 A의 특정한 약점을 집요하게 추궁하기 때문이라고 가정해 보겠습니다.)
A, B, C의 Elo Rating 을 각각 4500, 3550, 3144 로 설정해 놓고,
같은 비율로 충분히 많은 시합을 시킬 경우에 각각의 레이팅은 몇점이 될까요? -
1
세상의모든계산기
통계적 접근
- 1라운드당 3경기로 구성하여 각각 1회씩 대결 (순차적)
(기대 승률에 기반하여 Random 하게 승/패 결정. 무승부 없음.) - 매 경기 직후 ELO Rating 변경 (K=16)
- 100 라운드(=300경기) 진행 후 A, B, C 의 Rating 값 저장
- 5000 회 반복하여 통계분석
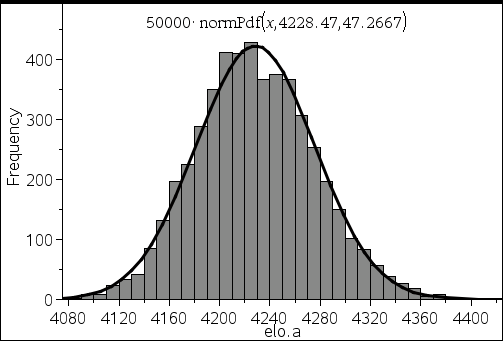
A : 4500에서 4228.47로 (▼271.53)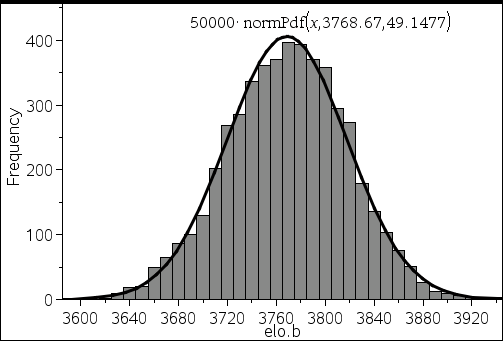
B : 3550에서 3768.67로 (▲218.67)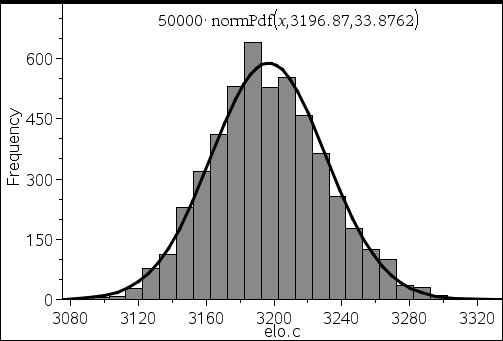
C : 3144에서 3196.87로 (▲52.87)- 조정 전 elo 합계 : 4500 + 3550 + 3144 = 11194
- 조정 후 elo 합계 : 4228.47+3768.67+3196.87 = 11194
- 1라운드당 3경기로 구성하여 각각 1회씩 대결 (순차적)
- 1



세상의모든계산기 님의 최근 댓글
V2 갱신 (nonK / K-Type 통합형) 예전에는 직접 코드작성 + AI 보조 하여 프로그램 만들었었는데, 갈수록 복잡해져서 손 놓고 있었습니다. 이번에 antigravity 설치하고, 테스트 겸 새로 V2를 올렸습니다. 직접 코드작성하는 일은 전혀 없었고, 바이브 코딩으로 전체 작성했습니다. "잘 했다 / 틀렸다 / 계산기와 다르다." "어떤 방향에서 코드 수정해 봐라." AI가 실물 계산기 각정 버튼의 작동 방식에 대한 정확한 이해는 없는 상태라서, V1을 바탕으로 여러차례 수정해야 했습니다만, 예전과 비교하면 일취월장 했고, 훨씬 쉬워졌습니다. 2026 02.04 A) 1*3*5*7*9 = 계산 945 B) √ 12번 누름 ㄴ 12회 해도 되고, 14회 해도 되는데, 횟수 기억해야 함. ㄴ 횟수가 너무 적으면 오차가 커짐 ㄴ 결과가 1에 매우 가까운 숫자라면 된 겁니다. 1.0016740522338 C) - 1 ÷ 5 + 1 = 1.0003348104468 D) × = 을 (n세트) 반복해 입력 ㄴ 여기서 n세트는, B에서 '루트버튼 누른 횟수' 3.9398949655688 빨간 부분 숫자에 오차 있음. (소숫점 둘째 자리 정도까지만 반올림 해서 답안 작성) 참 값 = 3.9362834270354... 2026 02.04 1. 분모 먼저 계산 400 × 10000 = 100 × 6000 = GT 결과값 4,600,000 역수 처리 ÷÷== 결과값 0.00000021739 2. 분자 곱하기 ×3 00 00 00 ×4 00 ×1 00 00 최종 결과 = 2,608,695.65217 2026 02.04 해결 방법 1. t=-1 을 기준으로 그래프를 2개로 나누어 표현 ㄴ 근데 이것도 tstep을 맞추지 않으면 문제가 발생할 것기도 하고, 상관이 없을 것 같기도 하고... 모르겠네요. 2. t=-1 이 직접 계산되도록 tstep을 적절하게 조정 tstep=0.1 tstep=0.01 도 해 보고 싶지만, 구간 크기에 따라 최소 tstep 이 변하는지 여기서는 0.01로 설정해도 0.015로 바뀌어버립니다. 그래서 tstep=0.02 로 하는게 최대한 긴 그래프를 얻을 수 있습니다. 2026 02.02 불연속 그래프 ti-nspire는 수학자처럼 연속적인 선을 그리는 것이 아니라, 정해진 `tstep` 간격으로 점을 찍고 그 점들을 직선으로 연결하는 'connect-the-dots' 방식으로 그래프를 그립니다. 여기에 tstep 간격에 따라 특이점(분모=0)이 제외되어 문제가 나타난 것입니다. seq(−2+0.13*t,t,0,23) {−2.,−1.87,−1.74,−1.61,−1.48,−1.35,−1.22,−1.09,−0.96,−0.83,−0.7,−0.57,−0.44,−0.31,−0.18,−0.05,0.08,0.21,0.34,0.47,0.6,0.73,0.86,0.99} t=-1 에서 그래프를 찾지 않습니다. 그 좌우 값인 −1.09, −0.96 두 값의 그래프값을 찾고, Window 범위를 보고 적당히 (연속되도록) 이어서 그래프를 완성하는 방식입니다. 그래서 t=-1에서도 그래프 값이 존재하는 것입니다. 2026 02.02