[일반 계산기] M 메모리 버튼(MR MC M+ M-)의 사용법
-
- 13시간 전 2015.01.14 - 22:31 36146 18
1. M 기능과 GT 기능의 비교
M 메모리는 (GT 메모리와 마찬가지로) 계산 결과를 저장하고 불러올 수 있는 공간입니다.
└ 일부에서는 M메모리를 "M통", GT메모리를 "GT통"으로 부르기도 합니다. 공식용어는 아닙니다.
M 과 GT 는 계산 결과를 일시적으로 기억(메모리)한다는 점에서 동일합니다.
차이점이 있다면, GT는 M의 심플버전이라는 점입니다. (심플하다=편하다+기능이 적다)
GT는 【=】 기호가 입력될 때 자동으로 더해지기만 합니다. 관련 버튼도 【GT】와 【=】 두개 뿐입니다.
M은 【M+】 또는 【M-】 를 누를 때만 메모리에 더해지거나 빼집니다. 버튼도 4개를 차지합니다. (기종에 따라 3개)
[참고] 
GT 기능 확인하러 가기
핵심 차이점
GT 메모리는 【=】 버튼을 누를 때 (필요하지 않을 때도) 자동으로 더해집니다. 자동이라서 더하기 싫어도 막을 방법이 없는 단점이 있습니다.
M 메모리는 '더하기(+)도 되고 빼기(-)도 된다'는 것과, '필요할 때만 메모리를 사용할 수 있는' 것이 장점입니다.
2. 계산기별 M 기능(버튼)의 차이
- 【M+】 【M-】 로 표시된 계산기도 있고,
【M+=】 【M-=】 로 표시된 계산기도 있습니다.
표기방식에 따른 차이가 있는 것 같진 않습니다만, 상수계산 중일 때 K Type vs NonK Type에 따라서 【=】가 먼저 실행되어 반복이 1회 추가되고 안되고의 차이가 있습니다. - 【MR】, 【MC】 로 표시하는 계산기도 있고, 거꾸로 CM, RM 으로 표기하는 계산기도 있습니다. (기능 차이는 없습니다)
- 【MR】, 【MC】 이 분리되지 않고 합쳐진 【MRC】 버튼만 있는 계산기도 있습니다.
【MRC】 버튼은 한번 누르면 MR로, 그대로 다시 한번 누르면 MC 로 동작합니다.
3. 사용법 예시
- "1 - 2×3 + 4×5×6 + 7 - 8×9 = ?"를 계산해 보자. (정답 : 50)
- GT 를 이용할 때 입력 순서 (CASIO 류, K-Type)
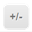
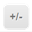
GT 결과값 = 50,
-
비교) 결과값 = 183
-
SHARP 류, Non-K Type의 계산기에서. 상수계산 방식의 차이 때문.
이 때는 【7】【=】 대신에 【7】【×】【1】【=】 또는 【7】【+】【0】【=】 으로 입력. - M 메모리 이용시 입력순서
* 결과값 = 50 (
)
* 이 때는 계산기 종류와 관계 없이 모두 동일한 결과.
더하기만 있을 때는 GT가 짱이지만, 이렇게 중간에 빼기가 들어가면 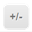때문에 입력이 매끄럽지 않을 수 있습니다. 그런 경우에는 【M+】, 혹은 【M-】 버튼을 이용하는 것이 직관적일 수 있겠습니다.
4. M 저장값 지우기 (아래 방법 중 택1)
- 【MC】 혹은 【CM】 이라고 적힌 키를 누르면, M 값이 초기화되어 지워집니다.
【MRC】 버튼이 있는 경우에는 2번 연속 눌러야 합니다. - 【AC】 를 누를 때 M에 저장된 값이 0 으로 초기화되며 M이 사라지는데, 그렇지 않은 계산기도 있습니다.
- 【MR】 【M-】 : 현재 M에 저장된 값을 불러내고, 그 값을 M에서 빼서 저장. 0 이 저장되면서 초기화 됩니다.
계산기에 M 마크가 없어졌다면 M 값이 초기화된 것입니다.
계산 시작 전에 항상 M 메모리가 비워져 있는지 확인해야 합니다.
5. 주의사항 (윈도우 내장 계산기)
윈도우(윈도우7 기준)에 내장된 계산기의 M기능은 연산중인 경우에도 연산의 결과가 아닌 현재 화면에 표시되어 있는 숫자만을 대상으로 M 기능이 작동합니다. 따라서 연산의 결과를 M에 적용시키려면 먼저 
를 눌러서 연산을 마쳐야만 합니다.
-
25
댓글18
- 1
-
세상의모든계산기
예시2 : 30000÷(1.08)^3 + 40000÷(1.08)^4 + 50000÷(1.08)^5 = ?
K Type :
【MC】
【1.08】【÷】【÷】
【30000】【=】【=】【M+】
【40000】【=】【=】【=】【M+】
【50000】【=】【=】【=】【=】【M+】
【MR】결과 87,245.32NonK Type :
【CM】
【30000】【÷】【1.08】【=】【=】【=】【M+】
【40000】【=】【=】【=】【=】【M+】
【50000】【=】【=】【=】【=】【=】【M+】
【RM】결과 87,245.32 - 1
- 2
- 1
- 2
- 1
- 2
-
세상의모든계산기
https://kin.naver.com/qna/detail.naver?d1id=4&dirId=40105&docId=433739025&page=1#answer1
M 메모리 기능과,
GT 메모리 기능이 같이 있는 계산기라면 계산 가능합니다.
1. 앞쪽 큰 덩어리 분모 5.6/6.7 + 7.8/8.9 를 GT에 저장
5.6 ÷ 6.7 =
7.8 ÷ 8.9 =
GT 결과 1.7122
2. 앞쪽 큰 분자를 +- 로 구분하여 순서대로 계산 후 M에 저장
1.2 ÷ 2.3 ÷ GT → M+
3.4 ÷ 4.5 ÷ GT → M+
3. GT를 초기화(0으로 만들기)
GT 2번 연타 (계산기마다 다를 수 있음)
4. 뒷쪽 큰덩어리에 대해서 앞의 1과 2 과정을 반복
5. 최종 M 저장된 값 확인 RM
-
세상의모든계산기
상수계산 기능과 M 메모리 기능 동시 사용시
계산 수식 : $ -100,000 + \dfrac{43,950}{1.2^{4}} \approx −78,804.98$
Non-K 계산기 : 【100000】【M-】【43950】【÷】【1.2】【=】【=】【=】【=】【M+】【MR】
카시오 K 계산기 : 【100000】【M-】【1.2】【÷】【÷】【43950】【=】【=】【=】【M+】【MR】 // = 횟수 3회 주의
계산 수식 : $ -100,000+\sum_{n=1}^{4}{\left( \dfrac{43,950}{1.2^{n}}\right)} \approx 13,774.88 $
Non-K 계산기 : 【100000】【M-】【43950】【÷】【1.2】【=】【=】【=】【=】【GT】【M+】【MR】
카시오 K 계산기 : 【100000】【M-】【1.2】【÷】【÷】【43950】【M+】【M+】【M+】【M+】【MR】
-
1
세상의모든계산기
-4,614.46 x 0.1 / (1 - (1/(1+0.10)^10)
https://allcalc.org/46323 일반 계산기로 복잡한 수식을 계산할 때의 버튼 입력 순서를 결정하는 방법
1/(1+0.10)^10 에서 1 나누기 1.1을 열번 하는것이 아닌 카시오 계산기에서 1.1을 먼저 나누고 1을 누른 후 =를 9번 누르나요?
https://allcalc.org/2335 [일반 계산기] 상수계산 - 카시오 K-Type (K-타입)
ㄴ 천천히 읽어보면서, 하나씩 따라해 보세요. - 1
- 2
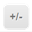버튼이 따로 있습니다. (+ 버튼도 아니고, - 버튼도 아닙니다)
세상의모든계산기 님의 최근 댓글
V2 갱신 (nonK / K-Type 통합형) 예전에는 직접 코드작성 + AI 보조 하여 프로그램 만들었었는데, 갈수록 복잡해져서 손 놓고 있었습니다. 이번에 antigravity 설치하고, 테스트 겸 새로 V2를 올렸습니다. 직접 코드작성하는 일은 전혀 없었고, 바이브 코딩으로 전체 작성했습니다. "잘 했다 / 틀렸다 / 계산기와 다르다." "어떤 방향에서 코드 수정해 봐라." AI가 실물 계산기 각정 버튼의 작동 방식에 대한 정확한 이해는 없는 상태라서, V1을 바탕으로 여러차례 수정해야 했습니다만, 예전과 비교하면 일취월장 했고, 훨씬 쉬워졌습니다. 2026 02.04 A) 1*3*5*7*9 = 계산 945 B) √ 12번 누름 ㄴ 12회 해도 되고, 14회 해도 되는데, 횟수 기억해야 함. ㄴ 횟수가 너무 적으면 오차가 커짐 ㄴ 결과가 1에 매우 가까운 숫자라면 된 겁니다. 1.0016740522338 C) - 1 ÷ 5 + 1 = 1.0003348104468 D) × = 을 (n세트) 반복해 입력 ㄴ 여기서 n세트는, B에서 '루트버튼 누른 횟수' 3.9398949655688 빨간 부분 숫자에 오차 있음. (소숫점 둘째 자리 정도까지만 반올림 해서 답안 작성) 참 값 = 3.9362834270354... 2026 02.04 1. 분모 먼저 계산 400 × 10000 = 100 × 6000 = GT 결과값 4,600,000 역수 처리 ÷÷== 결과값 0.00000021739 2. 분자 곱하기 ×3 00 00 00 ×4 00 ×1 00 00 최종 결과 = 2,608,695.65217 2026 02.04 해결 방법 1. t=-1 을 기준으로 그래프를 2개로 나누어 표현 ㄴ 근데 이것도 tstep을 맞추지 않으면 문제가 발생할 것기도 하고, 상관이 없을 것 같기도 하고... 모르겠네요. 2. t=-1 이 직접 계산되도록 tstep을 적절하게 조정 tstep=0.1 tstep=0.01 도 해 보고 싶지만, 구간 크기에 따라 최소 tstep 이 변하는지 여기서는 0.01로 설정해도 0.015로 바뀌어버립니다. 그래서 tstep=0.02 로 하는게 최대한 긴 그래프를 얻을 수 있습니다. 2026 02.02 불연속 그래프 ti-nspire는 수학자처럼 연속적인 선을 그리는 것이 아니라, 정해진 `tstep` 간격으로 점을 찍고 그 점들을 직선으로 연결하는 'connect-the-dots' 방식으로 그래프를 그립니다. 여기에 tstep 간격에 따라 특이점(분모=0)이 제외되어 문제가 나타난 것입니다. seq(−2+0.13*t,t,0,23) {−2.,−1.87,−1.74,−1.61,−1.48,−1.35,−1.22,−1.09,−0.96,−0.83,−0.7,−0.57,−0.44,−0.31,−0.18,−0.05,0.08,0.21,0.34,0.47,0.6,0.73,0.86,0.99} t=-1 에서 그래프를 찾지 않습니다. 그 좌우 값인 −1.09, −0.96 두 값의 그래프값을 찾고, Window 범위를 보고 적당히 (연속되도록) 이어서 그래프를 완성하는 방식입니다. 그래서 t=-1에서도 그래프 값이 존재하는 것입니다. 2026 02.02